The metafor Package

One of the fundamental concepts underlying a meta-analysis is the idea of weighting: More precise estimates are given more weight in the analysis then less precise estimates. In 'standard' equal- and random-effects models (such as those that can be fitted with the rma() function), the weighting scheme is quite simple and covered in standard textbooks on meta-analysis. However, in more complex models (such as those that can be fitted with the rma.mv() function), the way estimates are weighted is more complex. Here, I will discuss some of those intricacies.

To start, let's discuss the standard models first. Here, we are meta-analyzing a set of independent estimates and so we can use the rma() function. For illustration purposes, I will use (once again) the BCG vaccine dataset. We start by computing the log risk ratios and corresponding sampling variances for the 13 trials included in this dataset.

library(metafor)
dat <- dat.bcg
dat <- escalc(measure="RR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat,
              slab=paste0(author, ", ", year))
dat

   trial               author year tpos  tneg cpos  cneg ablat      alloc      yi     vi
1      1              Aronson 1948    4   119   11   128    44     random -0.8893 0.3256
2      2     Ferguson & Simes 1949    6   300   29   274    55     random -1.5854 0.1946
3      3      Rosenthal et al 1960    3   228   11   209    42     random -1.3481 0.4154
4      4    Hart & Sutherland 1977   62 13536  248 12619    52     random -1.4416 0.0200
5      5 Frimodt-Moller et al 1973   33  5036   47  5761    13  alternate -0.2175 0.0512
6      6      Stein & Aronson 1953  180  1361  372  1079    44  alternate -0.7861 0.0069
7      7     Vandiviere et al 1973    8  2537   10   619    19     random -1.6209 0.2230
8      8           TPT Madras 1980  505 87886  499 87892    13     random  0.0120 0.0040
9      9     Coetzee & Berjak 1968   29  7470   45  7232    27     random -0.4694 0.0564
10    10      Rosenthal et al 1961   17  1699   65  1600    42 systematic -1.3713 0.0730
11    11       Comstock et al 1974  186 50448  141 27197    18 systematic -0.3394 0.0124
12    12   Comstock & Webster 1969    5  2493    3  2338    33 systematic  0.4459 0.5325
13    13       Comstock et al 1976   27 16886   29 17825    33 systematic -0.0173 0.0714

Variable yi contains the log risk ratios and variable vi the corresponding sampling variances.

We now fit equal- and random-effects models to these estimates.

res.ee <- rma(yi, vi, data=dat, method="EE")
res.re <- rma(yi, vi, data=dat)

Next, we extract the weights assigned to the estimates in these two models with the weights() function (the values are given in percent) and assemble these values in a matrix with two columns.

w.ee.re <- cbind(
paste0(formatC(weights(res.ee), format="f", digits=1, width=4), "%"),
paste0(formatC(weights(res.re), format="f", digits=1, width=4), "%"))

Finally, we create a forest plot of the estimates. We add a bit of space at the bottom (by adjusting ylim), add the summary estimates from the two models to the bottom (with the addpoly() function), and also add the weight information from the matrix above as additional elements to the plot (via the ilab and ilab.xpos arguments). Some extra column labels are added with text() and the segments() function is used to add the line under the 'Weights' column label.

forest(dat$yi, dat$vi, xlim=c(-11,5), ylim=c(-3,17), top=4,
       atransf=exp, at=log(c(1/16, 1/4, 1, 4, 8)), digits=c(2L,4L), 
       ilab=w.ee.re, ilab.lab=c("EE Model","RE Model"), ilab.xpos=c(-6,-4))
abline(h=0)
addpoly(res.ee, row=-1)
addpoly(res.re, row=-2)
text(-5, 16, "Weights", font=2)
segments(-7, 15.5, -3, 15.5)

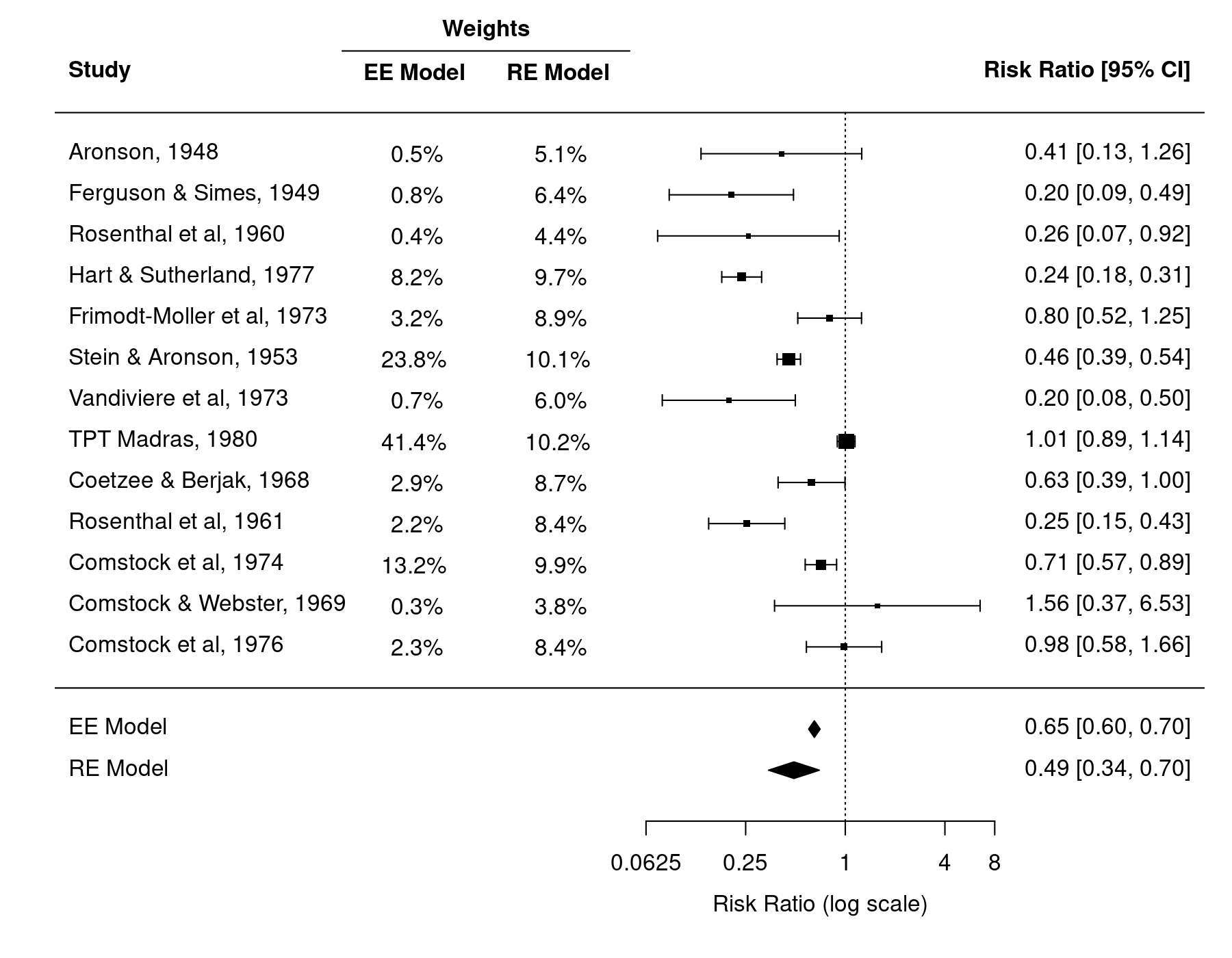
In the equal-effects model, the weights given to the estimates are equal to $w_i = 1 / v_i$, where $v_i$ is the sampling variance of the $i$th study. This is called 'inverse-variance weighting' and can be shown to be the most efficient way of weighting the estimates (i.e., the summary estimate has the lowest possible variance and is therefore most precise). As a result, the estimates with the lowest sampling variances, namely the ones from Stein and Aronson (1953), TPT Madras (1980), and Comstock et al (1974) are given considerably more weight than the rest of the studies.¹⁾ Together, these three studies receive almost 80% of the total weight and therefore exert a great deal of influence on the summary estimate. Especially the TPT Madras study 'pulls' the estimate to the right (closer to a risk ratio of 1).

In the RE model, the estimates are weighted with $w_i = 1 / (\hat{\tau}^2 + v_i)$. Therefore, not only the sampling variance, but also the (estimated) amount of heterogeneity (i.e., the variance in the underlying true effects) is taken into consideration when determining the weights. When $\hat{\tau}^2$ is large (relative to the size of the sampling variances), then the weights actually become quite similar to each other. Hence, smaller (less precise) studies may receive almost as much as weight as larger (more precise) studies. We can in fact see this happening in the present example. While the three studies mentioned above still receive the largest weights, their weights are now much more similar to those of the other studies. As a result, the summary estimate is not as strongly pulled to the right by the TPT Madras study.

The weights used in equal- and random-effects models are the inverse of the model-implied variances of the observed outcomes. For example, in the RE model, the model considers two sources of variability that affect the observed outcomes: sampling variability ($v_i$) and heterogeneity ($\hat{\tau}^2$). The sum of these two sources of variability is $\hat{\tau}^2 + v_i$ and the weights are therefore $w_i = 1 / (\hat{\tau}^2 + v_i)$. The summary estimate is then simply the weighted average of the estimates, namely $$\hat{\mu} = \frac{\sum_{i=1}^k w_i y_i}{\sum_{i=1}^k w_i}.$$ By comparing

wi <- 1 / (res.re$tau2 + dat$vi)
sum(wi * dat$yi) / sum(wi)

[1] -0.7145323

with the summary estimate from the random-effects model, namely

coef(res.re)

[1] -0.7145323

we can see that this is correct.

Models fitted with the rma.mv() function will typically be more complex than those fitted with rma().²⁾ In particular, they will usually involve multiple random effects and possibly correlated sampling errors. See Konstantopoulos (2011) and Berkey et al. (1998) for two illustrative examples. I will use the former example to discuss how the weighting works in such models.

The example involves studies that were conducted at schools that in turn were nested within a higher-ordering grouping variable (districts). This leads to a multilevel structure that we want to account for in the analysis. First, let's copy the data into dat (just to save some typing down the road) and examine the first 8 rows of the dataset. We see that there are 4 studies in the first and second district each.

dat <- dat.konstantopoulos2011
head(dat, 8)

   district school study year     yi    vi
1        11      1     1 1976 -0.180 0.118
2        11      2     2 1976 -0.220 0.118
3        11      3     3 1976  0.230 0.144
4        11      4     4 1976 -0.300 0.144
5        12      1     5 1989  0.130 0.014
6        12      2     6 1989 -0.260 0.014
7        12      3     7 1989  0.190 0.015
8        12      4     8 1989  0.320 0.024

Variable yi contains the standardized mean differences and vi the corresponding sampling variances. To analyze these data, we use a multilevel model with random effects for districts and schools within districts.

res <- rma.mv(yi, vi, random = ~ 1 | district/school, data=dat)
res

Multivariate Meta-Analysis Model (k = 56; method: REML)
 
Variance Components:
 
            estim    sqrt  nlvls  fixed           factor
sigma^2.1  0.0651  0.2551     11     no         district
sigma^2.2  0.0327  0.1809     56     no  district/school
 
Test for Heterogeneity:
Q(df = 55) = 578.8640, p-val < .0001
 
Model Results:
 
estimate      se    zval    pval   ci.lb   ci.ub
  0.1847  0.0846  2.1845  0.0289  0.0190  0.3504  *
 
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

The model now considers three sources of variability: Between-district heterogeneity ($\hat{\sigma}^2_1$), within-district heterogeneity ($\hat{\sigma}^2_2$), and sampling variability ($v_i$). The model-implied variances of the estimates are then the sum of these three sources of variability (i.e., $\hat{\sigma}^2_1 + \hat{\sigma}^2_2 + v_i$). However, the summary estimate from the model in not simply the weighted average of the estimates with weights given by $w_i = 1 / (\hat{\sigma}^2_1 + \hat{\sigma}^2_2 + v_i)$. This weighted average is:

wi <- 1 / (sum(res$sigma2) + dat$vi)
sum(wi * dat$yi) / sum(wi)

[1] 0.127597

But this is not equal to the summary estimate computed by rma.mv():

coef(res)

[1] 0.1847132

The two values are not the same, because the model also implies a certain amount of covariance between the effects, which is also taken into consideration when computing the summary estimate. We can examine the model implied marginal variance-covariance (var-cov) matrix of the estimates (or here, the first 8 rows and columns) with:

round(vcov(res, type="obs")[1:8,1:8], 3)

      1     2     3     4     5     6     7     8
1 0.216 0.065 0.065 0.065 0.000 0.000 0.000 0.000
2 0.065 0.216 0.065 0.065 0.000 0.000 0.000 0.000
3 0.065 0.065 0.242 0.065 0.000 0.000 0.000 0.000
4 0.065 0.065 0.065 0.242 0.000 0.000 0.000 0.000
5 0.000 0.000 0.000 0.000 0.112 0.065 0.065 0.065
6 0.000 0.000 0.000 0.000 0.065 0.112 0.065 0.065
7 0.000 0.000 0.000 0.000 0.065 0.065 0.113 0.065
8 0.000 0.000 0.000 0.000 0.065 0.065 0.065 0.122

The diagonal elements of this matrix are indeed equal to $\hat{\sigma}^2_1 + \hat{\sigma}^2_2 + v_i$:

round(sum(res$sigma2) + dat$vi[1:8], 3)

[1] 0.216 0.216 0.242 0.242 0.112 0.112 0.113 0.122

But there are also non-zero off-diagonal elements. In particular, note how the first two districts (with 4 estimates each) result in $4 \times 4$ blocks in this matrix. The off-diagonal elements in these blocks are covariances, which are equal to $\hat{\sigma}^2_1$ (i.e., the estimated between-district variance component) in this type of model. Hence, the first 6 rows and columns of the var-cov matrix are equal to $$M = \begin{bmatrix} \hat{\sigma}^2_1 + \hat{\sigma}^2_2 + v_1 & \hat{\sigma}^2_1 & \hat{\sigma}^2_1 & \hat{\sigma}^2_1 & & \\ \hat{\sigma}^2_1 & \hat{\sigma}^2_1 + \hat{\sigma}^2_2 + v_2 & \hat{\sigma}^2_1 & \hat{\sigma}^2_1 & & \\ \hat{\sigma}^2_1 & \hat{\sigma}^2_1 & \hat{\sigma}^2_1 + \hat{\sigma}^2_2 + v_3 & \hat{\sigma}^2_1 & & \\ \hat{\sigma}^2_1 & \hat{\sigma}^2_1 & \hat{\sigma}^2_1 & \hat{\sigma}^2_1 + \hat{\sigma}^2_2 + v_4 & & \\ & & & & \hat{\sigma}^2_1 + \hat{\sigma}^2_2 + v_5 & \hat{\sigma}^2_1 \\ & & & & \hat{\sigma}^2_1 & \hat{\sigma}^2_1 + \hat{\sigma}^2_2 + v_6 \\ \end{bmatrix}.$$ As in the documentation of the rma.mv() function (see help(rma.mv)), this matrix is referred to as $M$ (for the Marginal var-cov matrix of the estimates implied by the model).

To compute the summary estimate, we need to take the inverse of this matrix. As a result, we not only have weights, but actually an entire weight matrix. We can inspect this matrix (or the first 8 rows and columns) with:

round(weights(res, type="matrix")[1:8,1:8], 3)

       1      2      3      4      5      6      7      8
1  5.533 -1.102 -0.939 -0.939  0.000  0.000  0.000  0.000
2 -1.102  5.533 -0.939 -0.939  0.000  0.000  0.000  0.000
3 -0.939 -0.939  4.857 -0.801  0.000  0.000  0.000  0.000
4 -0.939 -0.939 -0.801  4.857  0.000  0.000  0.000  0.000
5  0.000  0.000  0.000  0.000 16.664 -4.733 -4.633 -3.898
6  0.000  0.000  0.000  0.000 -4.733 16.664 -4.633 -3.898
7  0.000  0.000  0.000  0.000 -4.633 -4.633 16.412 -3.817
8  0.000  0.000  0.000  0.000 -3.898 -3.898 -3.817 14.414

Since the var-cov matrix is 'block-diagonal', each block in the weight matrix is actually the inverse of the corresponding block from the $M$ matrix (you can check this for example for the first district with round(solve(vcov(res, type="obs")[1:4,1:4]), 3)).

Let $W = M^{-1}$ denote the weight matrix. Also, let $X$ denote the model matrix, which contains the values of the variables corresponding to the fixed effects. In the present case, the model just contains an intercept term and no further predictors/moderators and hence the model matrix is a single column of 1s (which can be extracted with model.matrix(res)). Finally, let $y$ denote the (column) vector with the estimates. Then the fixed effects are estimated with $$b = (X'WX)^{-1} X'Wy.$$ This is a so-called generalized least squares (GLS) estimator. For the present model, this yields a single number, namely the estimated intercept (i.e., the pooled/summary estimate). We can check that this works by manually crunching through the matrix algebra.³⁾

W <- weights(res, type="matrix")
X <- model.matrix(res)
y <- cbind(dat$yi)
solve(t(X) %*% W %*% X) %*% t(X) %*% W %*% y

[1] 0.1847132

This is indeed the same value as we obtained above with coef(res).

For those less familiar with matrix algebra, the equation that provides the summary estimate for such an 'intercept-only model' can also be written in the more familiar summation notation. Let $w_{ij}$ denote the element in the $i$th row and $j$th column of the weight matrix and let $y_i$ denote the $i$th estimate (with $i = 1, \ldots, k$). Then $$\hat{\mu} = \frac{\sum_{i=1}^k (\sum_{j=1}^k w_{ij}) y_i}{\sum_{i=1}^k \sum_{j=1}^k w_{ij}}.$$ The denominator of this fraction is just the sum of all elements in the weight matrix. In the numerator, we sum up the weights in each column of the weight matrix (which is the same as taking the sum in each row, since the weight matrix is symmetric) and multiply this sum by the corresponding estimate. This is done for each estimate and the resulting values are summed up. Let's check again that this is correct:

W <- weights(res, type="matrix")
sum(rowSums(W) * dat$yi) / sum(W)

[1] 0.1847132

While rowSums(W) takes the sum of all weight values in each row, most of those values are actually zeros. Hence, for each estimate, we really just need to sum up the values that are part of the block to which an estimate belongs. For example, for the first estimate (i.e., dat$yi[1]), we just need to sum up the first four values in the first row, that is, we would sum up:

W[1,1:4]

         1          2          3          4
 5.5325581 -1.1015344 -0.9394859 -0.9394859

For the second estimate, we would sum up W[2,1:4]. For the fifth estimate (which belongs to the second district), we would sum up W[5,5:8]. And so on.

If we look at the equation above again, we should note that $\hat{\mu}$ is actually still a weighted average of the estimates, but now the weight given to the $i$th estimate is equal to $\sum_{j=1}^k w_{ij}$. These 'row-sum weights' can be obtained with:

weights(res, type="rowsum")[1:8]

       1        2        3        4        5        6        7        8
1.824641 1.824641 1.556215 1.556215 2.430599 2.430599 2.379682 2.002198

They are given as percentages. We can use these weights to compute the weighted average of the estimates, which again yields the summary estimate:

wi <- weights(res, type="rowsum")
sum(wi * dat$yi) / sum(wi)

[1] 0.1847132

By examining the weight matrix, we can also build some intuition how the model accounts for multiple estimates coming from the same district. Note that the off-diagonal elements in the blocks of the weight matrix are negative. This results in a certain amount of downweighting of the estimates, so that districts contributing many estimates do not automatically receive tons of weight when computing the summary estimate. To illustrate this, we can compute the sum of the row-sum weights within each district. In addition, the table below shows how many estimates each district contributes.

data.frame(k = c(table(dat$district)),
           weight = tapply(wi, dat$district, sum))

     k    weight
11   4  6.761714
12   4  9.243078
18   3  8.536540
27   4  9.506693
56   4  9.502062
58  11 10.328499
71   3  8.943803
86   8 10.320158
91   6  9.883123
108  5  9.203041
644  4  7.771289

While district 58, which contributes 11 estimates, does receive the most weight, this is closely followed by district 86, which contributes 8 estimates. And not much further behind are districts 27 and 56, which 'only' contribute 4 estimates. This should alleviate, at least to some extent, worries that districts contributing many estimates are receiving 'too much weight' in the analysis.

Note that the degree of downweighting depends on the covariance between the estimates, which in the present model is simply the between-district heterogeneity. This variance component is quite large in the illustrative example (almost twice as large as the within-district heterogeneity; see res$sigma2[1] / res$sigma2[2]). In cases where this ratio is much smaller, clusters contributing many estimates will receive proportionally more weight (although the sampling variances also play a role here, so many imprecise estimates may still not receive much weight after all).

The example above shows that the weighting scheme underlying more complex models (that can be fitted with the rma.mv() function) is not as simple as in the 'standard' equal- and random-effects models (that can be fitted with the rma() function). Depending on the random effects included in the model (and the var-cov matrix of the sampling errors), the model may imply a certain degree of covariance between the estimates, which needs to be taken into consideration when estimating the fixed effects (e.g., the pooled/summary estimate) and their corresponding standard errors.

Note: James Pustejovsky has written up a very nice blog post which goes even deeper into this topic.

Berkey, C. S., Hoaglin, D. C., Antczak-Bouckoms, A., Mosteller, F., & Colditz, G. A. (1998). Meta-analysis of multiple outcomes by regression with random effects. Statistics in Medicine, 17(22), 2537–2550.

Konstantopoulos, S. (2011). Fixed effects and variance components estimation in three-level meta-analysis. Research Synthesis Methods, 2(1), 61–76.