Table of Contents
Funnel Plot with Limit Estimate
Description
Based on the regression test for funnel plot asymmetry, one can obtain a 'limit estimate' of the (average) true effect. The underlying idea is quite simple: When the standard error, sampling variance, or inverse (square root) sample size is used as the predictor for the regression test, the intercept of the model underlying the regression test in essence reflects the estimate under infinite precision. This is sometimes (cautiously) interpreted as an estimate of the (average) true effect that is adjusted for publication bias. The plot below shows a standard funnel plot (with the standard error on the y-axis) with the regression lines underlying the regression test superimposed (once using the standard errors and once using the sampling variances as predictor). The limit estimates are the predicted values for a standard error equal to 0 (i.e., at the top of the plot).
Plot
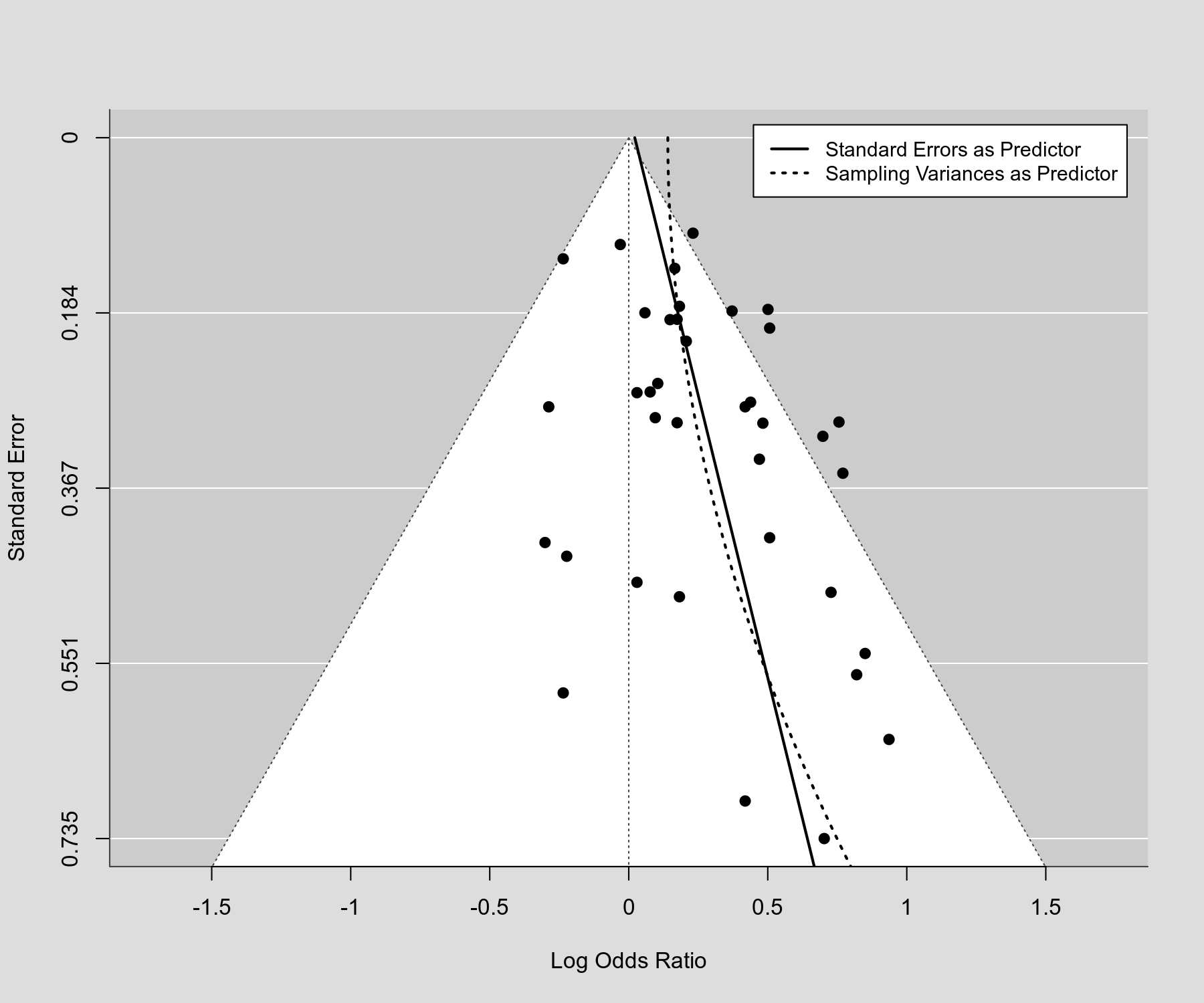
Code
library(metafor) ### fit random-effects model res <- rma(yi, vi, data=dat.hackshaw1998) ### funnel plot centered at 0 funnel(res, refline=0) ### regression test (by default using the standard error as predictor) reg <- regtest(res) ### add regression line to funnel plot se <- seq(0,0.8,length=100) lines(coef(reg$fit)[1] + coef(reg$fit)[2]*se, se) ### regression test (using the sampling variance as predictor) reg <- regtest(res, predictor="vi") ### add regression line to funnel plot (using the sampling variance as predictor) lines(coef(reg$fit)[1] + coef(reg$fit)[2]*se^2, se, lwd=2, lty="dotted") ### add legend legend("topright", inset=.02, lty=c("solid","dotted"), lwd=2, cex=0.9, bg="white", legend=c("Standard Errors as Predictor", "Sampling Variances as Predictor"))