This is an old revision of the document!
Table of Contents
van Houwelingen et al. (2002)
The Methods and Data
The article by van Houwelingen et al. (2002) is a sequel to the introductory article by Normand (1999) on methods for meta-analysis and focuses on more advanced techniques, such as meta-regression and bivariate/multivariate models. The authors mostly use SAS throughout the article for fitting the various models. The analyses are replicated here using R.
In the first part of the article, the models and methods are illustrated with data from 13 studies examining the effectiveness of the Bacillus Calmette-Guerin (BCG) vaccine for preventing tuberculosis (Colditz et al., 1994). The data are provided in Table I (p. 594) and can be loaded with:
library(metafor) dat <- dat.colditz1994 dat
(I copy the dataset into 'dat', which is a bit shorter and therefore easier to type further below). Variables tpos and tneg in this dataset indicate the number of individuals that were TB positive and negative in the vaccinated (treatment) group, while cpos and cneg indicate the number of individuals that were TB positive and negative in the non-vaccinated (control) group.
We can calculate the individual log odds ratios and corresponding sampling variances with:
dat <- escalc(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat)
In addition, we can recode the year variable as in the table with:
dat$year <- dat$year - 1900
The contents of the dataset are then:
trial author year tpos tneg cpos cneg ablat alloc yi vi 1 1 Aronson 48 4 119 11 128 44 random -0.9387 0.3571 2 2 Ferguson & Simes 49 6 300 29 274 55 random -1.6662 0.2081 3 3 Rosenthal et al 60 3 228 11 209 42 random -1.3863 0.4334 4 4 Hart & Sutherland 77 62 13536 248 12619 52 random -1.4564 0.0203 5 5 Frimodt-Moller et al 73 33 5036 47 5761 13 alternate -0.2191 0.0520 6 6 Stein & Aronson 53 180 1361 372 1079 44 alternate -0.9581 0.0099 7 7 Vandiviere et al 73 8 2537 10 619 19 random -1.6338 0.2270 8 8 TPT Madras 80 505 87886 499 87892 13 random 0.0120 0.0040 9 9 Coetzee & Berjak 68 29 7470 45 7232 27 random -0.4717 0.0570 10 10 Rosenthal et al 61 17 1699 65 1600 42 systematic -1.4012 0.0754 11 11 Comstock et al 74 186 50448 141 27197 18 systematic -0.3408 0.0125 12 12 Comstock & Webster 69 5 2493 3 2338 33 systematic 0.4466 0.5342 13 13 Comstock et al 76 27 16886 29 17825 33 systematic -0.0173 0.0716
Fixed-Effects Model
The first model considered is the fixed-effects model based on the log odds ratios. The same model can be fitted with:
res <- rma(yi, vi, data=dat, method="FE") res
Fixed-Effects Model (k = 13) Test for Heterogeneity: Q(df = 12) = 163.1649, p-val < .0001 Model Results: estimate se zval pval ci.lb ci.ub -0.4361 0.0423 -10.3190 <.0001 -0.5190 -0.3533 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
For easier interpretation, these results can be back-transformed to the odds ratio scale with:
predict(res, transf=exp, digits=3)
pred ci.lb ci.ub 0.647 0.595 0.702
These results correspond to those reported on pages 595-596.
Random-Effects Model
A random-effects model can be fitted (using maximum likelihood estimation) to the same data with:
res <- rma(yi, vi, data=dat, method="ML") res
Random-Effects Model (k = 13; tau^2 estimator: ML) tau^2 (estimated amount of total heterogeneity): 0.3025 (SE = 0.1549) tau (square root of estimated tau^2 value): 0.5500 I^2 (total heterogeneity / total variability): 91.23% H^2 (total variability / sampling variability): 11.40 Test for Heterogeneity: Q(df = 12) = 163.1649, p-val < .0001 Model Results: estimate se zval pval ci.lb ci.ub -0.7420 0.1780 -4.1694 <.0001 -1.0907 -0.3932 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Again, we can back-transform these results to the odds ratio scale:
predict(res, transf=exp, digits=3)
pred ci.lb ci.ub cr.lb cr.ub 0.476 0.336 0.675 0.153 1.478
These results correspond to those reported on pages 597-598.
Figure 1 in the article provides a plot of the profile likelihood function of the between-trial variance (i.e., $\tau^2$). The same figure can be obtained with:
profile(res, xlim=c(0.01,2), steps=100, log="x", cex=0, lwd=2) abline(h=logLik(res) - 1.92, lwd=2) abline(v=c(0.12, 0.89), lty="dashed")

The bounds of the 95% profile likelihood based confidence interval for $\tau^2$ are also added to the figure (i.e., .12 to .89). However, profile likelihood CIs for $\tau^2$ often do not have nominal coverage probabilities, especially when based on ML estimation (Viechtbauer, 2007). In this case, the interval is likely to be too narrow. On the other hand, CIs for $\tau^2$ obtained with the Q-profile method (Viechtbauer, 2007) typically do achieve nominal coverage probabilities. Such a CI can be easily obtained with:
confint(res)
estimate ci.lb ci.ub tau^2 0.3025 0.1302 1.1812 tau 0.5500 0.3608 1.0868 I^2(%) 91.2283 81.7376 97.5971 H^2 11.4003 5.4757 41.6169
The interval (i.e., 0.13 to 1.18) is quite a bit wider.1)
Constructing a profile likelihood plot (Figure 2 in the article) and corresponding CI for the mean treatment effect (i.e., $\mu$) is a bit more involved (see p. 598). However, as an alternative, I would suggest using the Knapp and Hartung method (Hartung & Knapp, 2001a, 2001b) for constructing the CI for $\mu$. It is known to achieve essentially nominal coverage in most circumstances (e.g., Hartung & Knapp, 2001a, 2001b; Sánchez-Meca & Marín-Martínez, 2008). This CI can be obtained with:
res <- rma(yi, vi, data=dat, method="ML", test="knha") predict(res, transf=exp, digits=3)
pred ci.lb ci.ub cr.lb cr.ub 0.476 0.318 0.714 0.134 1.687
This CI (i.e., .318 to .714) is just a bit wider than the profile likelihood CI reported in the paper (i.e., .323 to .691).
Figure 3 in the paper shows the observed log odds ratios with 95% CIs and the corresponding empirical Bayes estimates with 95% posterior confidence intervals. With a bit of work, the same figure can be created with:
res <- rma(yi, vi, data=dat, method="ML") sav <- blup(res) par(family="mono", mar=c(5,4,1,2)) forest(res, refline=res$b, addcred=TRUE, xlim=c(-7,8), alim=c(-3,3), slab=1:13, psize=0.8, ilab=paste0("(n = ", formatC(apply(dat[,c(4:7)], 1, sum), width=7, big.mark=","), ")"), ilab.xpos=-3.5, ilab.pos=2, rows=13:1+0.15, header="Trial (total n)") arrows(sav$pi.lb, 13:1 - 0.15, sav$pi.ub, 13:1 - 0.15, length=0.03, angle=90, code=3, lty="dotted") points(sav$pred, 13:1 - 0.15, pch=15, cex=0.8)

The credibility/prediction interval shown at the bottom (as the dotted line going through the summary polygon) is slightly wider than the one reported in the article, as it also takes the uncertainty in $\hat{\mu}$ into consideration. This interval (i.e., -1.875 to .391) can also be obtained with:
predict(res, digits=3)
pred se ci.lb ci.ub cr.lb cr.ub -0.742 0.178 -1.091 -0.393 -1.875 0.391
Bivariate Approach
In the next part of the article, the authors introduce the bivariate model for meta-analysis. For this purpose, the dataset is treated in a different way, with each study contributing two data points to the analysis, namely the outcome (i.e., log odds) of the vaccinated (treatment) group and the outcome (i.e., log odds) of the non-vaccinated (control) group. The L'Abbé plot makes this idea explicit (Figure 4 in the paper):
res <- rma(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat, method="ML") labbe(res, xlim=c(-7,-1), ylim=c(-7,-1), xlab="ln(odds) not-vaccinated group", ylab="ln(odds) vaccinated group")
The dashed line indicates the estimated effect based on the model.
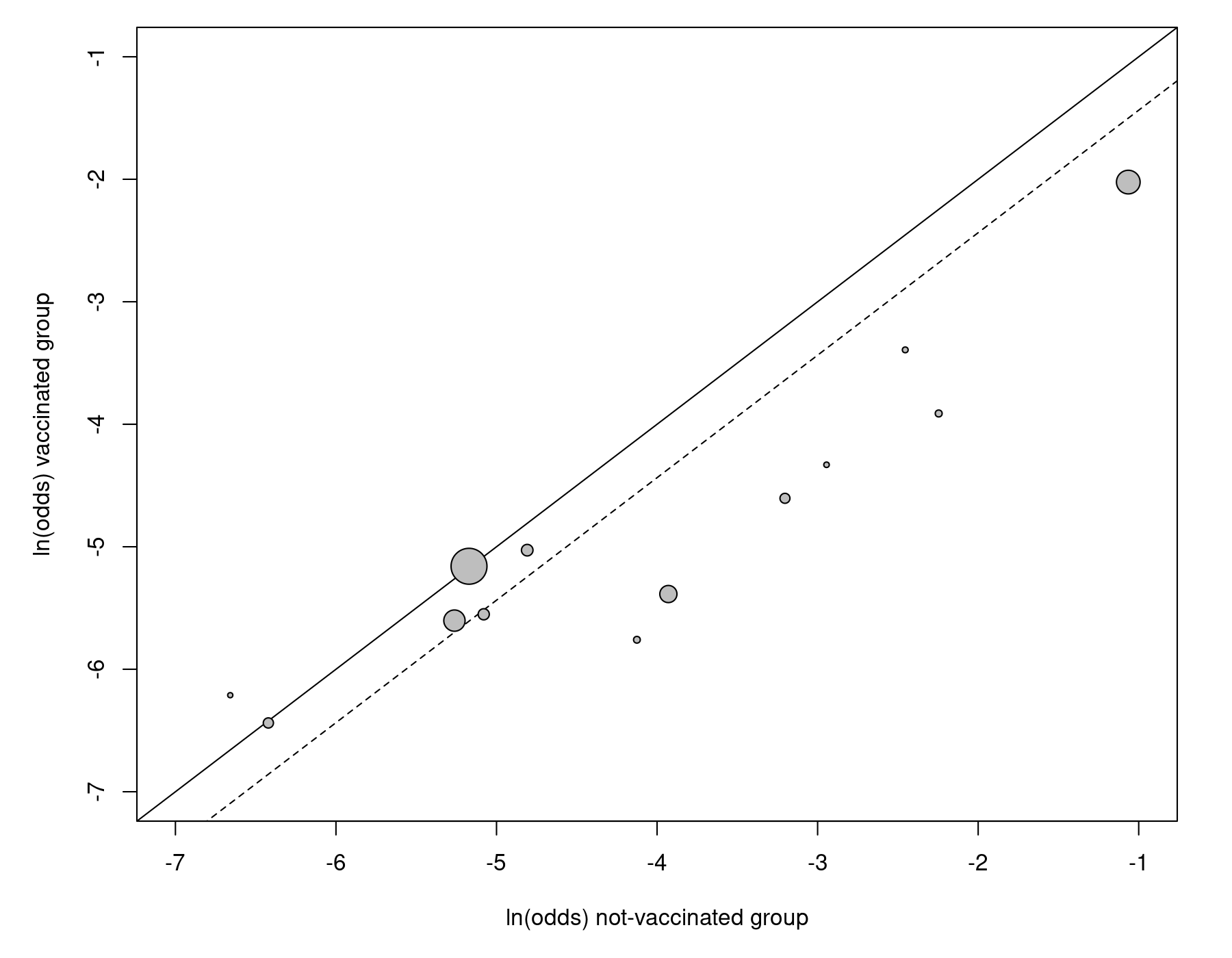
The dataset in the corresponding long format can be obtained with:
dat.long <- to.long(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat.colditz1994)
The arm-specific outcomes (i.e., log odds) with corresponding sampling variances can be added to the dataset with:
dat.long <- escalc(measure="PLO", xi=out1, mi=out2, data=dat.long) dat.long$tpos <- dat.long$tneg <- dat.long$cpos <- dat.long$cneg <- NULL levels(dat.long$group) <- c("EXP", "CON") dat.long$group <- relevel(dat.long$group, ref="CON") dat.long
trial author year ablat alloc study group out1 out2 yi vi 1 1 Aronson 1948 44 random 1 EXP 4 119 -3.3928 0.2584 2 1 Aronson 1948 44 random 1 CON 11 128 -2.4541 0.0987 3 2 Ferguson & Simes 1949 55 random 2 EXP 6 300 -3.9120 0.1700 4 2 Ferguson & Simes 1949 55 random 2 CON 29 274 -2.2458 0.0381 5 3 Rosenthal et al 1960 42 random 3 EXP 3 228 -4.3307 0.3377 6 3 Rosenthal et al 1960 42 random 3 CON 11 209 -2.9444 0.0957 7 4 Hart & Sutherland 1977 52 random 4 EXP 62 13536 -5.3860 0.0162 8 4 Hart & Sutherland 1977 52 random 4 CON 248 12619 -3.9295 0.0041 9 5 Frimodt-Moller et al 1973 13 alternate 5 EXP 33 5036 -5.0279 0.0305 10 5 Frimodt-Moller et al 1973 13 alternate 5 CON 47 5761 -4.8087 0.0215 11 6 Stein & Aronson 1953 44 alternate 6 EXP 180 1361 -2.0230 0.0063 12 6 Stein & Aronson 1953 44 alternate 6 CON 372 1079 -1.0649 0.0036 13 7 Vandiviere et al 1973 19 random 7 EXP 8 2537 -5.7593 0.1254 14 7 Vandiviere et al 1973 19 random 7 CON 10 619 -4.1255 0.1016 15 8 TPT Madras 1980 13 random 8 EXP 505 87886 -5.1592 0.0020 16 8 TPT Madras 1980 13 random 8 CON 499 87892 -5.1713 0.0020 17 9 Coetzee & Berjak 1968 27 random 9 EXP 29 7470 -5.5514 0.0346 18 9 Coetzee & Berjak 1968 27 random 9 CON 45 7232 -5.0796 0.0224 19 10 Rosenthal et al 1961 42 systematic 10 EXP 17 1699 -4.6046 0.0594 20 10 Rosenthal et al 1961 42 systematic 10 CON 65 1600 -3.2034 0.0160 21 11 Comstock et al 1974 18 systematic 11 EXP 186 50448 -5.6030 0.0054 22 11 Comstock et al 1974 18 systematic 11 CON 141 27197 -5.2621 0.0071 23 12 Comstock & Webster 1969 33 systematic 12 EXP 5 2493 -6.2118 0.2004 24 12 Comstock & Webster 1969 33 systematic 12 CON 3 2338 -6.6584 0.3338 25 13 Comstock et al 1976 33 systematic 13 EXP 27 16886 -6.4384 0.0371 26 13 Comstock et al 1976 33 systematic 13 CON 29 17825 -6.4211 0.0345
Since there is no overlap in the data used to calculate these arm-specific outcomes, the observed outcomes are (conditionally) independent. However, the corresponding true outcomes are likely to be correlated. The bivariate model allows us to estimate the variance and correlation of the true outcomes in the two arms:
res <- rma.mv(yi, vi, mods = ~ group - 1, random = ~ group | trial, struct="UN", data=dat.long, method="ML") res
Multivariate Meta-Analysis Model (k = 26; method: ML)
Variance Components:
outer factor: trial (nlvls = 13)
inner factor: group (nlvls = 2)
estim sqrt k.lvl fixed level
tau^2.1 2.4073 1.5516 13 no CON
tau^2.2 1.4314 1.1964 13 no EXP
rho.CON rho.EXP CON EXP
CON 1 0.9467 - no
EXP 0.9467 1 13 -
Test for Residual Heterogeneity:
QE(df = 24) = 5270.3863, p-val < .0001
Test of Moderators (coefficient(s) 1:2):
QM(df = 2) = 292.4633, p-val < .0001
Model Results:
estimate se zval pval ci.lb ci.ub
groupCON -4.0960 0.4347 -9.4226 <.0001 -4.9480 -3.2440 ***
groupEXP -4.8337 0.3396 -14.2329 <.0001 -5.4994 -4.1681 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
These are the same results are shown on page 604.
We can directly obtain the estimated (mean) log odds ratio from this model by not removing the intercept (and making the control group the reference level for the group factor):
res <- rma.mv(yi, vi, mods = ~ group, random = ~ group | trial, struct="UN", data=dat.long, method="ML")
The last part of the output is then:
Model Results:
estimate se zval pval ci.lb ci.ub
intrcpt -4.0960 0.4347 -9.4226 <.0001 -4.9480 -3.2440 ***
groupEXP -0.7378 0.1797 -4.1047 <.0001 -1.0901 -0.3855 ***
The estimate of $\mu$ (i.e., $-0.74$) is essentially the same as the one obtained earlier based on the random-effects model of the (log) odds ratios. Also, based on the bivariate model, we can estimate the amount of heterogeneity in the true log odds ratios with:
res$tau2[1] + res$tau2[2] - 2*res$rho*sqrt(res$tau2[1]*res$tau2[2])
[1] 0.3241742
This value is quite close to the estimate of $\tau^2$ obtained earlier.
Regression of True Log Odds
The results above show that the underlying true log odds in the vaccinated and unvaccinated groups are strongly correlated ($\hat{\rho} \approx 0.947$). As discussed in the article (p. 601), one can also derive the regression line when regressing the true log odds in the vaccinated on the true log odds in the unvaccinated group based on the results from the bivariate model. The slope of the regression line (and its standard error) can be obtained as follows:
res <- rma.mv(yi, vi, mods = ~ group - 1, random = ~ group | trial, struct="UN", data=dat.long, method="ML") b1 <- with(res, G["EXP","CON"] / G["CON","CON"]) ### ~ 0.730 (see page 605 in article) r <- with(res, G["EXP","CON"] / sqrt(G["EXP","EXP"] * G["CON","CON"])) se.b1 <- sqrt(with(res, G["EXP","EXP"]/G["CON","CON"] * (1-r^2) / (res$g.levels.comb.k - 2))) round(c(b1=b1, se.b1=se.b1, t=b1/se.b1, pval=2*pt(abs(b1/se.b1), df=res$g.levels.comb.k-2, lower.tail=FALSE)), 4)
b1 se.b1 t pval 0.7300 0.0749 9.7467 0.0000
We can calculate the intercept as follows.
b0 <- as.vector(coef(res)[2] - coef(res)[1] * b1) round(b0, 4)
[1] -1.8437
Then Figure 5 in the paper (p. 605) can be recreated with:
tmp <- rma(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat, method="FE") labbe(tmp, xlim=c(-8,0), ylim=c(-8,0), xlab="ln(odds) not-vaccinated group", ylab="ln(odds) vaccinated group", lty=c("dotted", "blank"), grid=TRUE) points(coef(res)[1], coef(res)[2], pch=19, cex=3) abline(a=b0, b=b1, lwd=3)
If the ellipse package is installed (install.packages("ellipse")), we can add the 95% coverage region/ellipse with:
library(ellipse) xy <- ellipse(res$G, centre=coef(res), level=0.95) lines(xy[,1],xy[,2], col="gray50")

Note: The ellipse shown in Figure 5 in the paper appears to be drawn incorrectly. In particular, it appear to be too wide along the y-axis. The following code shows that the ellipse drawn above has the correct width for one of the points.
x <- c(coef(res)[1], -3.89047055) c(t(x - coef(res)) %*% solve(res$G) %*% (x - coef(res))) abline(v=x[1]) abline(h=x[2])
Meta-Regression
It may be possible to account for (at least part of) the heterogeneity in the treatments effects (i.e., log odds ratios) based on one or more moderator variables (i.e., study characteristics that may influence the size of the effect). Such analyses are typically conducted with meta-regression models, as described in the article. For example, a meta-regression model which includes the absolute latitude of the study location as a predictor of the treatment effect can be fitted with:
res <- rma(yi, vi, mods = ~ ablat, data=dat, method="ML") res
Mixed-Effects Model (k = 13; tau^2 estimator: ML)
tau^2 (estimated amount of residual heterogeneity): 0.0040 (SE = 0.0086)
tau (square root of estimated tau^2 value): 0.0634
I^2 (residual heterogeneity / unaccounted variability): 9.71%
H^2 (unaccounted variability / sampling variability): 1.11
R^2 (amount of heterogeneity accounted for): 98.67%
Test for Residual Heterogeneity:
QE(df = 11) = 25.0954, p-val = 0.0088
Test of Moderators (coefficient(s) 2):
QM(df = 1) = 94.0098, p-val < .0001
Model Results:
estimate se zval pval ci.lb ci.ub
intrcpt 0.3710 0.1061 3.4963 0.0005 0.1630 0.5789 ***
ablat -0.0327 0.0034 -9.6959 <.0001 -0.0393 -0.0261 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
The same results are given on page 608.
Models with publication year, method of allocation, and the model including absolute latitude and publication year as predictors can be fitted with (output not shown):
rma(yi, vi, mods = ~ year, data=dat, method="ML") rma(yi, vi, mods = ~ alloc, data=dat, method="ML") rma(yi, vi, mods = ~ ablat + year, data=dat, method="ML")
The bivariate meta-regression model can be fitted with:
res <- rma.mv(yi, vi, mods = ~ group + group:I(ablat-33) - 1, random = ~ group | trial, struct="UN", data=dat.long, method="ML") res
Multivariate Meta-Analysis Model (k = 26; method: ML)
Variance Components:
outer factor: trial (nlvls = 13)
inner factor: group (nlvls = 2)
estim sqrt k.lvl fixed level
tau^2.1 1.1819 1.0872 13 no CON
tau^2.2 1.2262 1.1073 13 no EXP
rho.CON rho.EXP CON EXP
CON 1 1.0000 - no
EXP 1.0000 1 13 -
Test for Residual Heterogeneity:
QE(df = 22) = 2862.6396, p-val < .0001
Test of Moderators (coefficient(s) 1:4):
QM(df = 4) = 426.2408, p-val < .0001
Model Results:
estimate se zval pval ci.lb ci.ub
groupCON -4.1174 0.3061 -13.4529 <.0001 -4.7172 -3.5175 ***
groupEXP -4.8257 0.3129 -15.4240 <.0001 -5.4389 -4.2125 ***
groupCON:I(ablat - 33) 0.0725 0.0219 3.3057 0.0009 0.0295 0.1154 ***
groupEXP:I(ablat - 33) 0.0391 0.0224 1.7471 0.0806 -0.0048 0.0830 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
The same results are given on pages 612-613. Note that absolute latitude was centered at 33 degrees, as was done by the authors. The model does converge without any difficulties, despite the very high correlation (which is essentially indistinguishable from 1).
The difference in slopes can be directly obtained with:
res <- rma.mv(yi, vi, mods = ~ group*I(ablat-33), random = ~ group | trial, struct="UN", data=dat.long, method="ML")
The results are the same as before, except for the last part, which is now equal to:
Model Results:
estimate se zval pval ci.lb ci.ub
intrcpt -4.1174 0.3061 -13.4529 <.0001 -4.7172 -3.5175 ***
groupEXP -0.7083 0.0481 -14.7301 <.0001 -0.8026 -0.6141 ***
I(ablat - 33) 0.0725 0.0219 3.3057 0.0009 0.0295 0.1154 ***
groupEXP:I(ablat - 33) -0.0333 0.0028 -11.6988 <.0001 -0.0389 -0.0277 ***
Random-Effects Conditional Logistic Model
On page 616, the authors describe the possibility of analyzing these data with a (random-effects) conditional logistic model. More details on this approach can be found in Stijnen, Hamza, and Ozdemir (2010) and van Houwelingen, Zwinderman, and Stijnen (1993). The results for this model are not given in the paper, but can be obtained with:
res <- rma.glmm(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat, model="CM.EL", method="ML") res
Random-Effects Model (k = 13; tau^2 estimator: ML) Model Type: Conditional Model with Exact Likelihood tau^2 (estimated amount of total heterogeneity): 0.3116 (SE = 0.1612) tau (square root of estimated tau^2 value): 0.5582 I^2 (total heterogeneity / total variability): 91.46% H^2 (total variability / sampling variability): 11.72 Tests for Heterogeneity: Wld(df = 12) = 202.1150, p-val < .0001 LRT(df = 12) = 176.8738, p-val < .0001 Model Results: estimate se zval pval ci.lb ci.ub -0.7538 0.1801 -4.1862 <.0001 -1.1067 -0.4009 *** --- Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Some patience is required when fitting this model. Since the sample sizes of the individual studies are quite large, the results are very similar to those obtained earlier using the "normal-normal" model.
Mixture Model
Instead of assuming normally distributed random effects, an alternative analysis approach is to estimate the components of a non-parametric mixture. For more details, see page 617 in the article and the references provided therein. For illustration purposes, the results given in the article can be obtained with the CAMAN package:
library(CAMAN) res <- mixalg(obs="yi", var="vi", data=dat) res
Computer Assisted Mixture Analysis:
Data consists of 13 observations (rows).
The Mixture Analysis identified 4 components of a gaussian distribution:
DETAILS:
p mean
1 0.3552377 -1.457730429
2 0.1505239 -0.967784453
3 0.2979943 -0.329557291
4 0.1962441 0.002256384
Log-Likelihood: -8.324311 BIC: 34.60327
A four-point mixture is obtained. The mean and variance implied by this mixture are:
sum(res@p * res@t)
[1] -0.7612789
and
sum(res@p * (res@t - sum(res@p*res@t))^2)
[1] 0.348674
respectively. The mean and variance agree quite well with the random-effects model assuming normally distributed true effects.
Multiple Outcomes
When multiple outcomes are measured based on the same sample of subjects within a study, we can again use a multivariate model for the analysis, but now the correlation among the observed outcomes needs to be accounted for. The authors illustrate such an analysis with the data from Berkey et al. (1998). Please follow the link for more details on analyzing such data (including a reproduction of the results given on pages 617-620).
References
Berkey, C. S., Hoaglin, D. C., Antczak-Bouckoms, A., Mosteller, F., & Colditz, G. A. (1998). Meta-analysis of multiple outcomes by regression with random effects. Statistics in Medicine, 17(22), 2537–2550.
Colditz, G. A., Brewer, T. F., Berkey, C. S., Wilson, M. E., Burdick, E., Fineberg, H. V., & Mosteller, F. (1994). Efficacy of BCG vaccine in the prevention of tuberculosis: Meta-analysis of the published literature. Journal of the American Medical Association, 271(9), 698–702.
Hartung, J., & Knapp, G. (2001a). A refined method for the meta-analysis of controlled clinical trials with binary outcome. Statistics in Medicine, 20(24), 3875–3889.
Hartung, J., & Knapp, G. (2001b). On tests of the overall treatment effect in meta-analysis with normally distributed responses. Statistics in Medicine, 20(12), 1771–1782.
van Houwelingen, H. C., Arends, L. R., & Stijnen, T. (2002). Advanced methods in meta-analysis: Multivariate approach and meta-regression. Statistics in Medicine, 21(4), 589–624.
van Houwelingen, H. C., Zwinderman, K. H., & Stijnen, T. (1993). A bivariate approach to meta-analysis. Statistics in Medicine, 12(24), 2273–2284.
Sánchez-Meca, J., & Marín-Martínez, F. (2008). Confidence intervals for the overall effect size in random-effects meta-analysis. Psychological Methods, 13(1), 31–48.
Stijnen, T., Hamza, T. H., & Ozdemir, P. (2010). Random effects meta-analysis of event outcome in the framework of the generalized linear mixed model with applications in sparse data. Statistics in Medicine, 29(29), 3046–3067.
Viechtbauer, W. (2007). Confidence intervals for the amount of heterogeneity in meta-analysis. Statistics in Medicine, 26(1), 37–52.